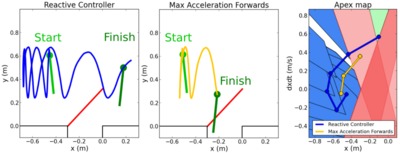
We propose the idea of a discrete navigation problem – consisting of controlling the state of a discrete-time control system to reach a goal set while in the interim avoiding a set of obstacle states – to approximate a simplified class of transitional legged robotic tasks such as leaping which have no well established mathematical description that lends itself to synthesis. The control relation given in Theorem 1 is (assuming a task solution exists) necessary and sufficient to solve a discrete navigation problem in a minimum number of steps, and is well suited to computation when a legged system’s continuous-time within-stride controller anchors sufficiently simple stance mechanics. We demonstrate the efficacy of this control technique on a physical hopping robot affixed to a boom to reactively leap over an obstacle with a running start, controlling in continuous time during stance to exhibit a linear stance map.