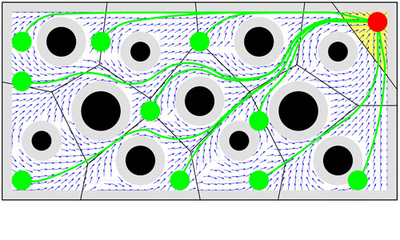
We reconsider the problem of reactive navigation in sphere worlds, i.e., the construction of a vector field over a compact, convex Euclidean subset punctured by Euclidean disks, whose flow brings a Euclidean disk robot from all but a zero measure set of initial conditions to a designated point destination, with the guarantee of no collisions along the way. We use power diagrams, generalized Voronoi diagrams with additive weights, to identify the robot’s collision free convex neighborhood, and to generate the value of our proposed candidate solution vector field at any free configuration via evaluation of an associated convex optimization problem. We prove that this scheme generates a continuous flow with the specified properties. We also propose its practical extension to the nonholonomically constrained kinematics of the standard differential drive vehicle.
For more information: Kod*lab