What follows is a brief overview of my paper with Eric Swenson (BYU):
[1] “A `transversal’ for minimal invariant sets in the boundary of a CAT(0) group” with Eric L. Swenson (Brigham Young University), Trans. Amer. Math. Soc. 365 (2013), 3069-3095.
The rank rigidity problem for CAT(0) groups in its boundary form was introduced by Ballmann and Buyalo, and asks whether (1) an infinite group G acting properly and co-compactly on a CAT(0) space X whose visual boundary ∂X has Tits-diameter diam(∂X)>π must contain a rank one element; and (2) in the case that the visual boundary of X has diameter π, is this boundary a spherical building?
Ballman and Buyalo show that diam(∂X)>2π implies the presence of rank one elements in G. Later work by Swenson and Papasoglu improves this bound to 3π/2.
In our attempt at problems (1) and (2), we observe that the Ellis action of the Stone-Cech compactification βG of G on the cone boundary ∂X is a semigroup action by Lip-1 endomorphisms when ∂X is taken with the Tits metric, and derive some new structural results about minimal invariant sets of the G-action on the cone boundary.
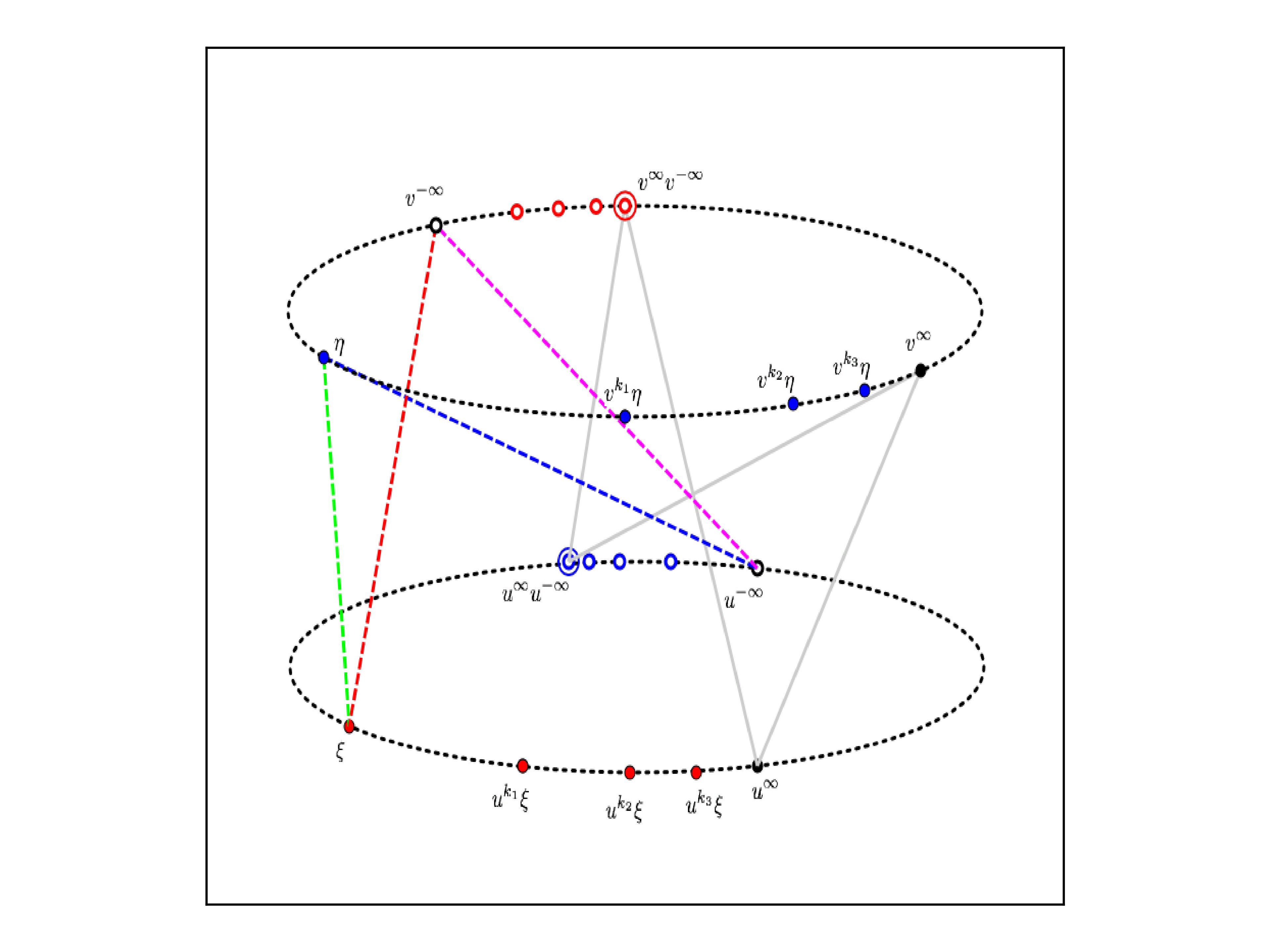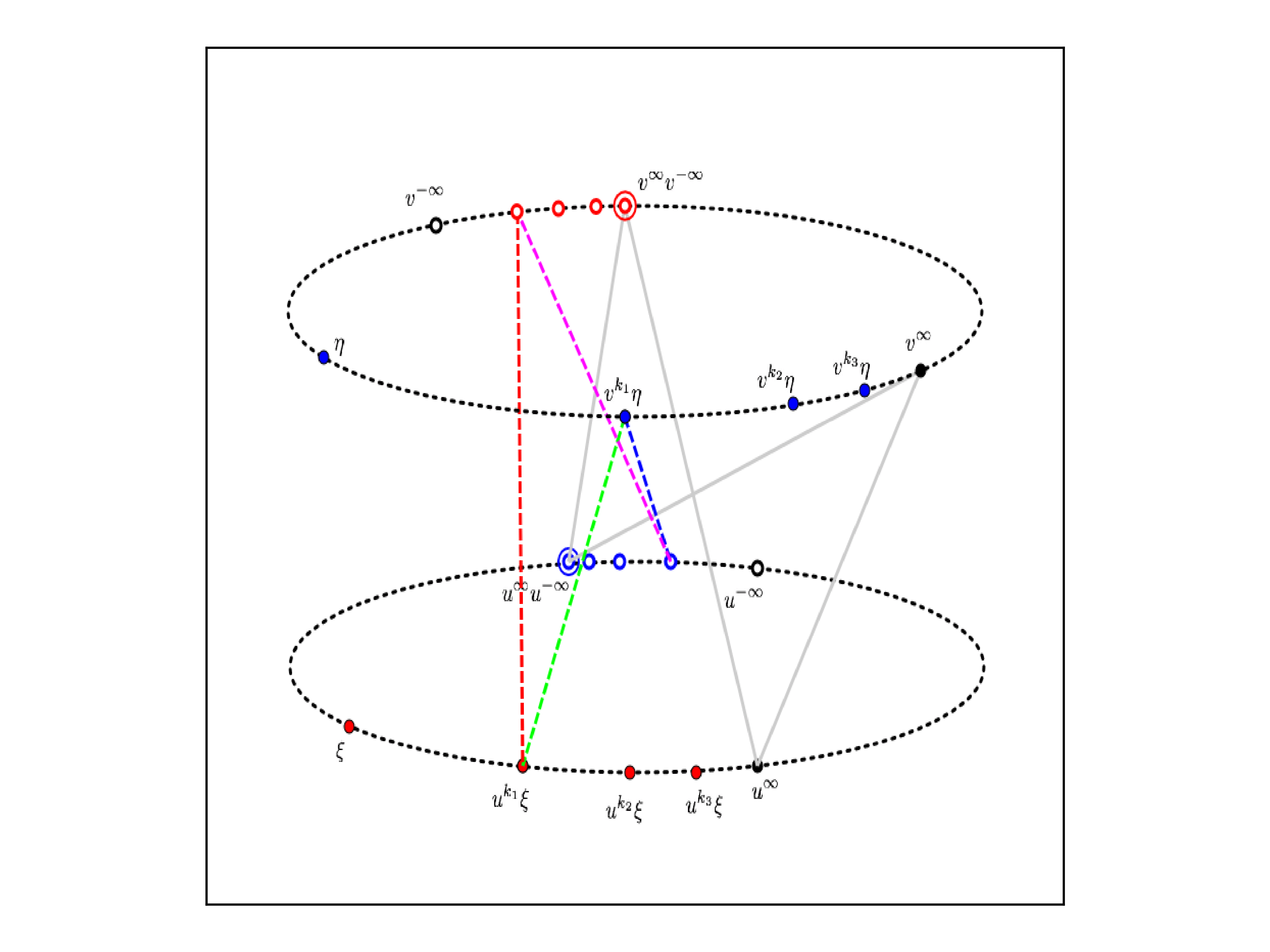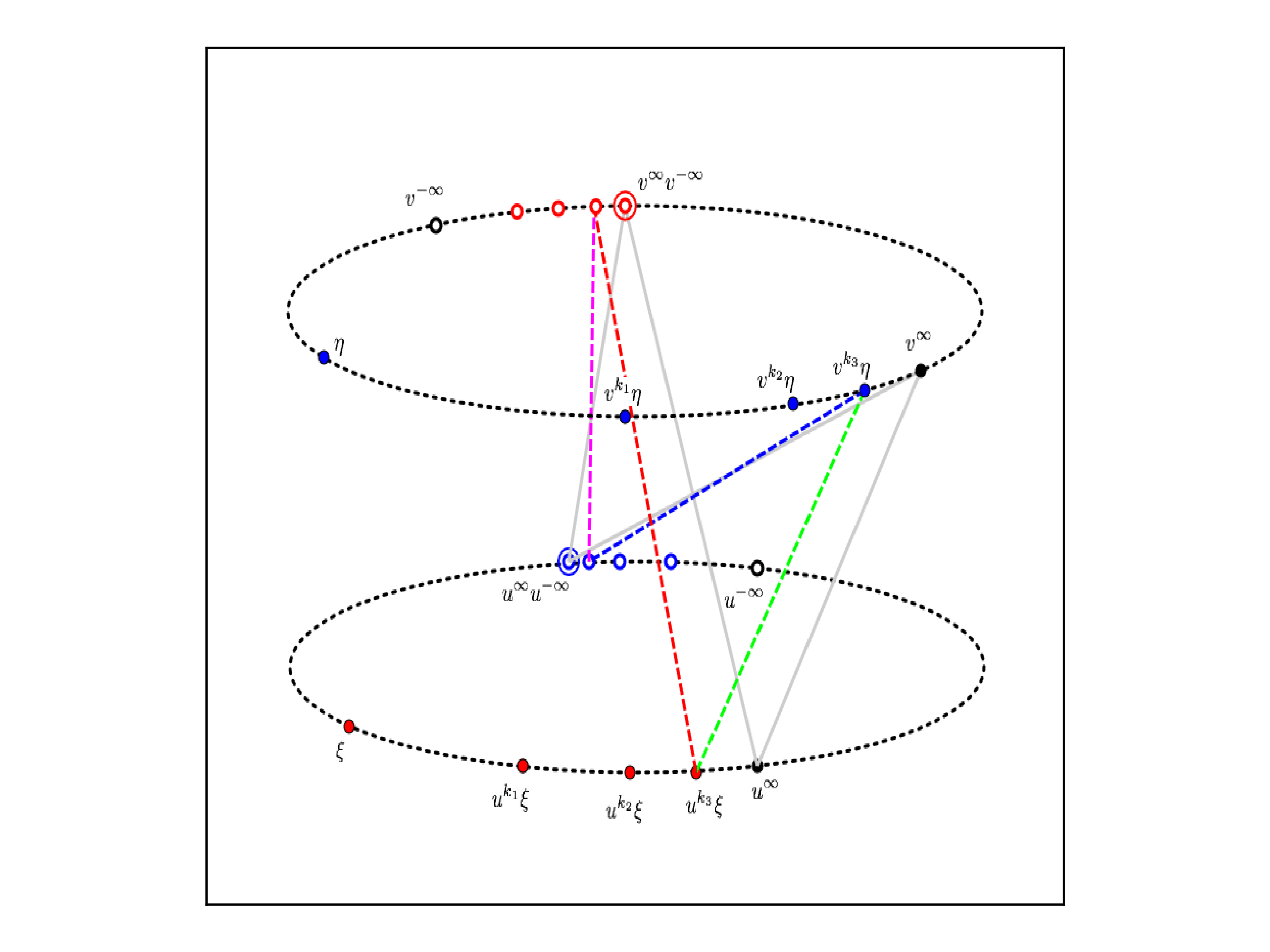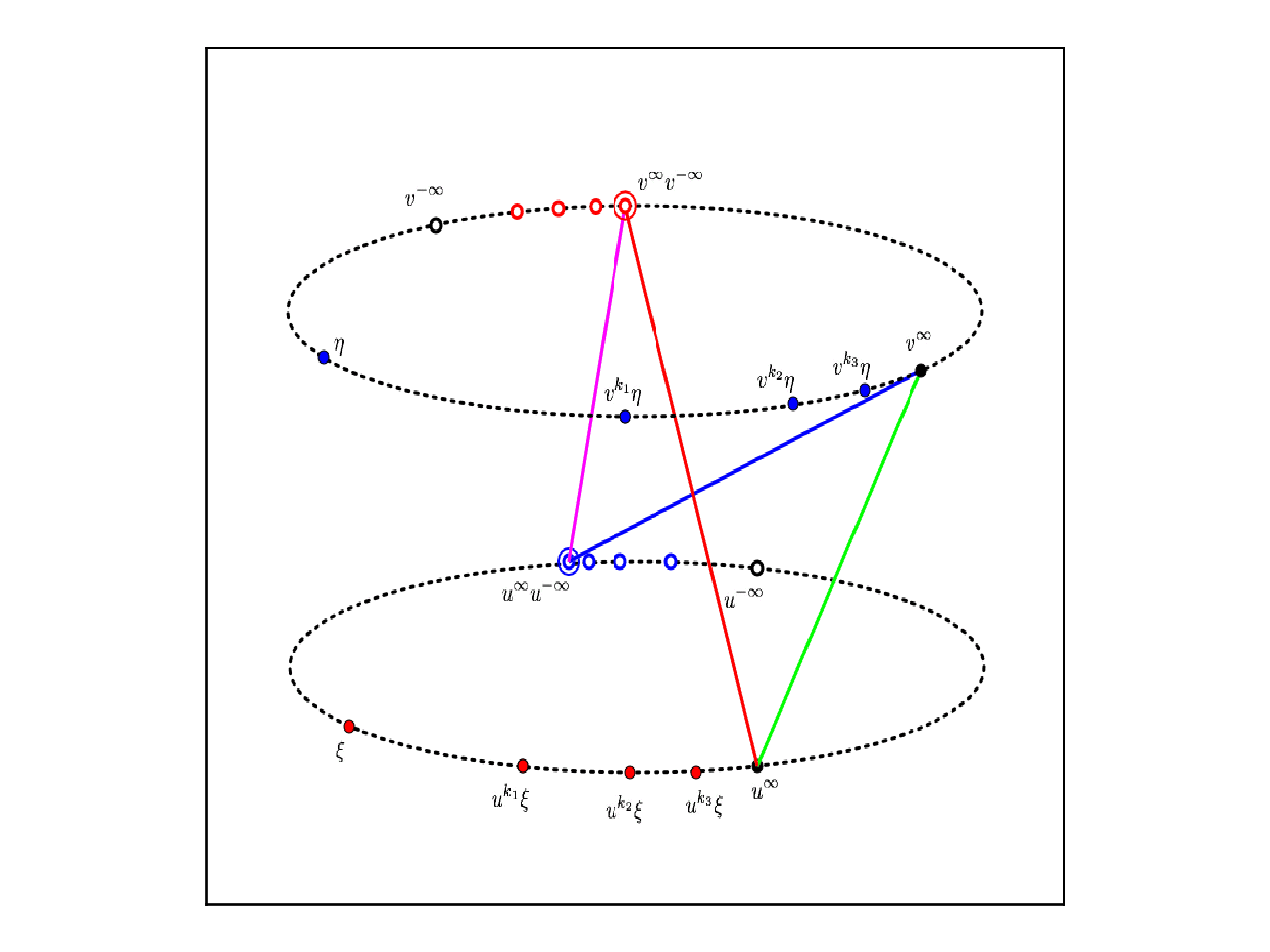
In a nutshell, a pair of points p,q in ∂X is said to be compressible, if
∃ω∈βG dist(ωp,ωq)<dist(p,q) .
We are interested in the maximal G-incompressible subsets of ∂X, because of the intuitive idea that:
1. If G has rank one elements, then non-degenerate incompressible subsets should not exist;
2. If ∂X is a building, then the maximal G-incompressible subsets are natural candidates for being simplices of the building structure.
The animated figure above illustrates a compression in the boundary of the product of two copies of a non-abelian free group.
So far, our approach allowed us to improve the Swenson-Papasoglu bound to a bound dependent on the geometric dimension of diam(∂X), and results in a characterization of Bieberbach groups as CAT(0) groups with no proximal pairs in their Tits boundary.
Press here for my presentation of this work to the Penn Geometry & Topology seminar back in 2012. Also take a look at recent work by Ricks building on ours, studying CAT(0) groups with 1-dimensional boundaries.
