The utility of artificial potential functions is explored as a means of translating automatically a robot task description into a feedback control law to drive the robot actuators. A class of functions is sought which will guide a point robot amid any finite number of spherically bounded obstacles in Euclidean n-space toward an arbitrary destination point. By introducing a set of additional constraints, the subclass of navigation functions is defined. This class is dynamically sound in the sense that the actual mechanical system will inherit the essential aspects of the qualitative behavior of the gradient lines of the cost function. An existence proof is given by constructing a one parameter family of such functions; the parameter is used to guarantee the absence of local minima.
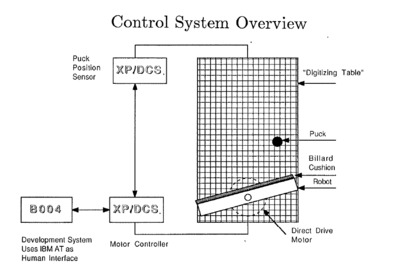
Distributed Control System for a Juggling Robot

The juggling work takes its place within a larger program of research concerned with the development of unified methodologies for robot task representation, planning, and control. The talk will summarize this large context, and then provide a more detailed look at progress in juggling to date.
For more information: Kod*Lab
Robotics in an Intermittent Dynamical Environment: A Prelude to Juggling
We explore a very simple representative of a class of of robotic tasks which require “dynamic dexterity”, among them the task of “juggling”. In this initial paper we propose a formal definition of a “vertical one juggle”, report a few preliminary analytical results, and offer illustrative simulations. This analysis is being currently applied to the design of and experimentation with “juggling algorithms” for a one-degree of freedom “robot” operative in the gravitational field.
Adaptive Techniques for Mechanical Systems
Strict Lyapunov functions are constructed for a class of nonlinear feedback compensated mechanical systems, requiring no à priori information concerning the initial conditions of the closed-looped system. These Lyapunov functions may be used to design a stable adaptive version of the “computed-torque” algorithm for tracking a reference trajectory. A particular Lyapunov function is then generalized to permit an adaptive version of control scheme forced by reference dynamics rather than reference trajectory.
Quadratic Lyapunov Functions for Mechanical Systems
The “mechanical systems” define a large and important class of highly nonlinear dynamical equations which, for example, encompasses all robots. In this report it is shown that a strict Lyapunov Function suggested by the simplest examplar of the class – a one degree of freedom linear time invariant dynamical system – may be generalized over the entire class. The report lists a number of standard but useful consequences of this discovery. The analysis suggests that the input-output properties of the entire class of nonlinear systems share many characteristics in common with those of a second order, phase canonical, linear time invariant differential equation.
For more information: Kod*Lab
Exact robot navigation by means of potential functions: Some topological
The limits in global navigation capability of potential function based robot control algorithms are explored. Elementary tools of algebraic and differential topology are used to advance arguments suggesting the existence of potential functions over a bounded planar region with arbitrary fixed obstacles possessed of a unique local minimum. A class of such potential functions is constructed for certain cases of a planar disk region with an arbitrary number of smaller disks removed.
Lyapunov Analysis of Robot Motion
The practice of automatic control has its origins in antiquity. It is only recently – within the middle decades of this century – that a body of scientific theory has been developed inform and improve that practice. Control theorists tend to divide their history into two periods. A “classical” period, prior to the sixties witnessed the systematization of feedback techniques based upon frequency domain analysis dominated by applications to electronics and telephony. A “modern” period in the sixties and seventies was characterized by a growing concern with formal analytical techniques pursued within the time domain motivated by the more stringent constraints posed by space applications and the enhanced processing capability of digital technology. The hallmark of control theory has been, by and large, a systematic exploitation of the properties of linear dynamical systems whether in the frequency or time domain. The dynamical behavior of mechanical systems appears to depart dynamically from the familiar linear case. The intent of this article is to show that a systematic application of Lyapunov Theory affords qualitative understanding of certain aspects of the input/output properties of a broad class of nonlinear systems (which includes all robots) analogous to that available for linear time invariant systems. For concreteness, this discussion is limited to robot arms – open kinematic chains with rigid links.
High Gain Feedback and Telerobotic Tracking
Asymptotically stable linear time invariant systems are capable of tracking arbitrary reference signals with a bounded error proportional to the magnitude of the reference signal (and its derivatives). It is shown that a similar property holds for a general class of nonlinear dynamical systems which includes all robots. As in the linear case, the error bound may be made “arbitrarily” small by increasing the magnitude of the feedback gains which stabilize the system.
Robot Control: Theoretical Foundations and Recent Trends
Automatic Planning and Control of Robot Natural Motion Via Feedback
A feedback control strategy for the command of robot motion includes some limited automatic planning capabilities. These may be seen as sequential solution algorithms implemented by the robot arm interpreted as a mechanical analog computer. This perspective lends additional insight into the manner in which such control techniques may fail, and motivates a fresh look at requisite sensory capabilities.
For more information: Kod*Lab