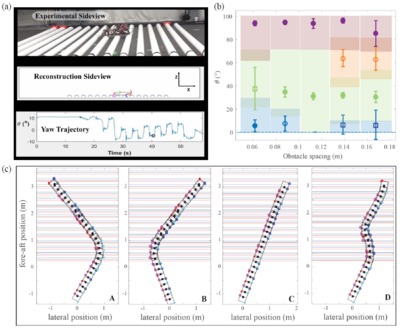
We study a quadrupedal robot traversing a structured (i.e., periodically spaced) obstacle field driven by an open-loop quasi-static trotting walk. Despite complex, repeated collisions and slippage between robot legs and obstacles, the robot’s horizontal plane body orientation (yaw) trajectory can converge in the absence of any body level feedback to stable steady state patterns. We classify these patterns into a series of “types” ranging from stable locked equilibria, to stable periodic oscillations, to unstable or mixed period oscillations. We observe that the stable equilibria can bifurcate to stable periodic oscillations and then to mixed period oscillations as the obstacle spacing is gradually increased. Using a 3D-reconstruction method, we experimentally characterize the robot leg-obstacle contact configurations at each step to show that the different steady patterns in robot orientation trajectories result from a self-stabilizing periodic pattern of leg-obstacle contact positions. We present a highly-simplified coupled oscillator model that predicts robot orientation pattern as a function of the leg-obstacle contact mechanism. We demonstrate that the model successfully captures the robot steady state for different obstacle spacing and robot initial conditions. We suggest in simulation that using the simplified coupled oscillator model we can create novel control strategies that allow multi-legged robots to exploit obstacle disturbances to negotiate randomly cluttered environments. For more information: Kod*lab (link to kodlab.seas.upenn.edu)