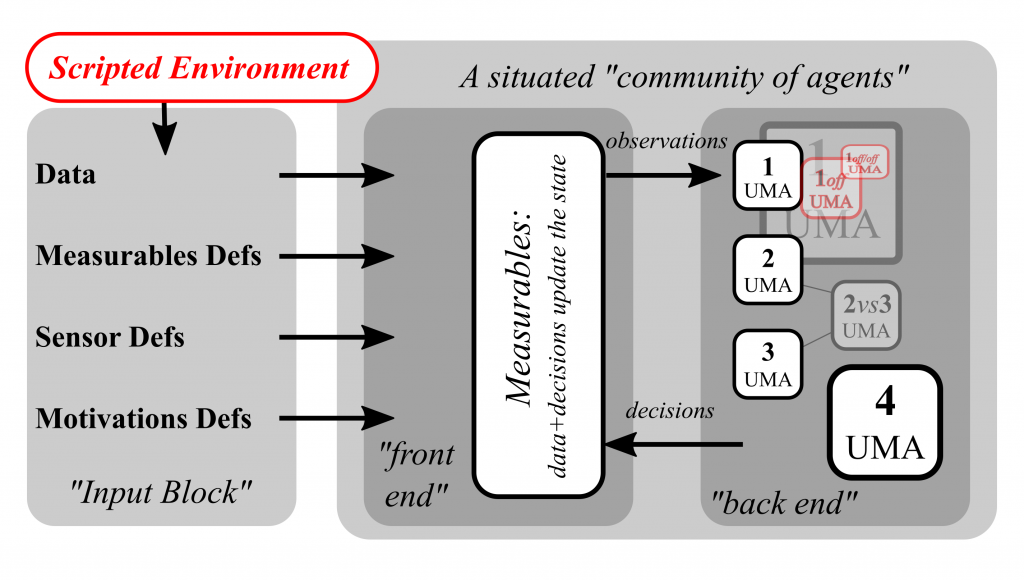
What is UMCA?
A major obstacle on the way to producing general autonomous agents is the problem of maintaining a scalable internal representation of the agent’s experiences, reasoning and predictions. Existing approaches to this problem, ranging from cognitive architectures (SOAR, ACT-R) through MDP/POMDP/SMDP solvers and to modern Deep Learning networks are challenged by at least one of: (1) the necessity to provide a-priori limited models of the interactions between the agent and its environment; (2) high-dimensional data structures incurring prohibitive maintenance costs, and/or (3) mathematical opacity of the representation denying the designer any ability to provide formal performance guarantees regarding what precisely has been learnt by the agent.
In his book “The Society of Mind”, Marvin Minsky studies a hypothetical model of human cognition, presenting an alternative approach to understanding general agency (related notions are Minsky’s k-lines, and Louis Narens’ notion of local complementation).
The fundamental units are “agents”, who act on the human subject’s surroundings by mobilizing additional agents of the same kind, who act on the human’s world by mobilizing yet other agents… eventually distributing the task at hand to the “end-effector” agents, the ones actually doing something tangible with the human subject’s body (e.g. excite a muscle fiber), causing it to interact with the world in the required way. Minsky ingests a great deal of observations from studies of cognitive development in children and synthesizes a hypothetical way of structuring the interactions among his “agents”, producing a model with the power to explain many interesting phenomena of human cognition.
Minsky admits, however, that his theory lacks a rigorous mathematical foundation explaining how his “agents” come to be. An overwhelming majority of the task examples he considers will be recognized as high-level tasks by a modern roboticist, involving multiple layers of representation and control: “build a tower of blocks”, “build an arch made of blocks”… The question of how his intertwined hierarchical structures of agents self-assemble from the lowest level motor actions — how they grow and adapt themselves to the human subject’s environment, eventually assuming their “proper” final shape and the patterns of interaction postulated by the theory — remains unanswered.
An attempt at forming a self-assembling computational structure of this kind was made by Drescher, bearing some similarity with ours, but the work lacks a formal description of the resulting internal representation, making it hard to study emergent dynamics and the discrepancy between the actual situation space and the one “imagined” by the agent. Drescher also admits that his system’s capacity for generalization (through his notion of schema reification) is insufficient for a host of generalization tasks considered necessary for a general learner.
Further developments of these ideas by Minsky, in the book “The Emotion Machine”, provide insight as to how control/decision-making may be facilitated by multiple interacting motivations (by the way, take a look at Paul Reverdy’s page on the subject of motivational dynamics), but the mathematical foundations of the theory remain undealt with.
The over-arching purpose of the UMCA project, in a nutshell, is to finish the mathematical homework we inherited from Minsky. We seek to endow a robot with a “Society of Minds”-like memory-and-control architecture, whose process of self-assembly is completely derived from the history of its motor actions and on sensory data in the form of raw bit-streams, having provided the robot with no prior model of its situation space. Assuming that teachers are available in some form, we would like such a robot to be capable of learning to execute known tasks in varying circumstances (including unexpected ones). Crucially, emphasis on scalability and on the mathematical quantification of the quality and information content of the evolving internal representations are corner stones of UMCA: the individual agents maintain simplistic, but informative representations which facilitate greedy reactive control based on relative information gradients, while deliberation among agents is used to overcome both well-understood deficiencies of the individual representations and the problem of conflicting predictions.
What follows is a preview of UMCA based on the accounts given in:
[1] “Toward a memory model for autonomous topological mapping and navigation: The case of binary sensors and discrete actions” (Dan P.Guralnik and Daniel E. Koditschek) in Communication, Control, and Computing (Allerton), 2012 50th Annual Allerton Conference on, pp. 936–945, IEEE 2012.
[2] “Universal Memory Architectures for Autonomous Machines,” (Dan P. Guralnik and Daniel E. Koditschek), technical report (2016)
[3] “Iterated Belief Revision Under Resource Constraints: Logic as Geometry” (Dan P. Guralnik and Daniel E. Koditschek), preprint (2018)
Universal Memory Architecture (UMA): The Basics
Funded in part by AFOSR CHASE MURI and in part by NSF-CABiR
Topological inspiration.
UMA is a relaxation of the idea, coming from Topology, that a space X could be reconstructed, up to homotopy equivalence, from the combinatorics of intersections of a sufficiently tame covering:
Maintaining a data structure to encode a (possibly changing) nerve is too expensive (exponential in the number of sensors), except if some simplifying assumptions are present (in applications, X is often planar and the covering is by convex/star-shaped sets). Moreover, since nerves are arbitrary simplicial complexes, motion planning in this model is computationally infeasible.
Restricting Attention to Pairwise Conjunctions.
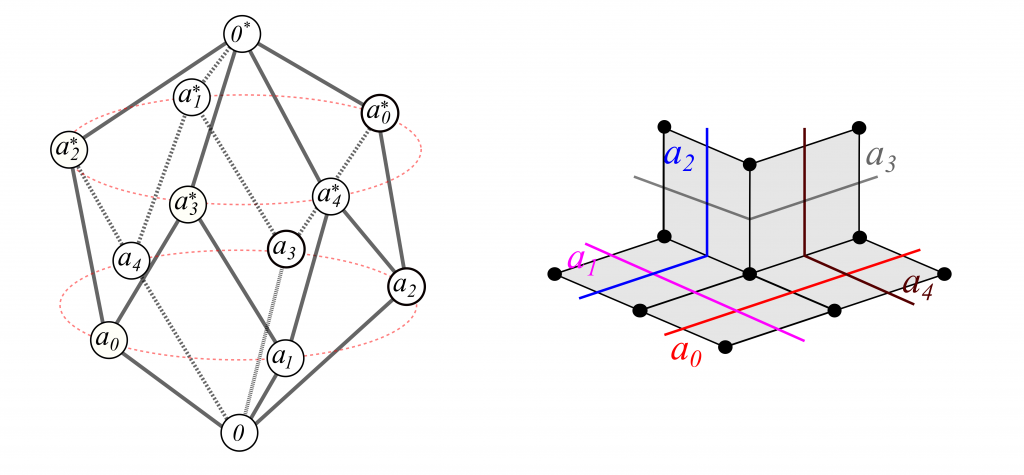
Restricting attention to edges in the nerve — to pairwise intersections — is equivalent to studying implications: if sensor a has activation field A in X, and sensor b has activation field B in X then,
A and B are disjoint ⇔ A is contained in X-B ⇔ a implies ¬b.
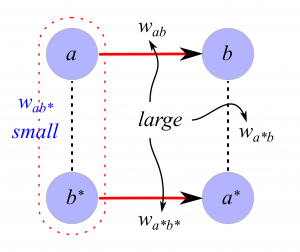
It turns out that, by maintaining and continually updating our degree of certainty regarding statements of this form for every pair a,b of sensors in an agent’s sensorium Σ, an UMA agent learns a contractible (“hole-free”) geometric representation of X. Extending the sensorium to include a sensor a*, the complementary sensor to a, for each a∈Σ, gives rise to a directed graph Γ encoding a record of implications to facilitate the UMA agent’s reasoning (figure on left). However, more turns out to be true: it also encodes a cubical complex which can serve as a model space for any realization of the sensors in Σ, as long as the implications recorded in the graph hold true among the activation fields in X. This property is what the word “universal” in UMA stands for.
Universal World Models from a Record of Implications.
In [1] we describe the general procedure for obtaining a model space M from the record of implications Γ, inspired by Sageev-Roller Duality, and prove a general theorem identifying sufficient conditions on the sensorium to ensure the recovery of the homotopy type of X from M via the removal of all vertices that are not witnessed in X.
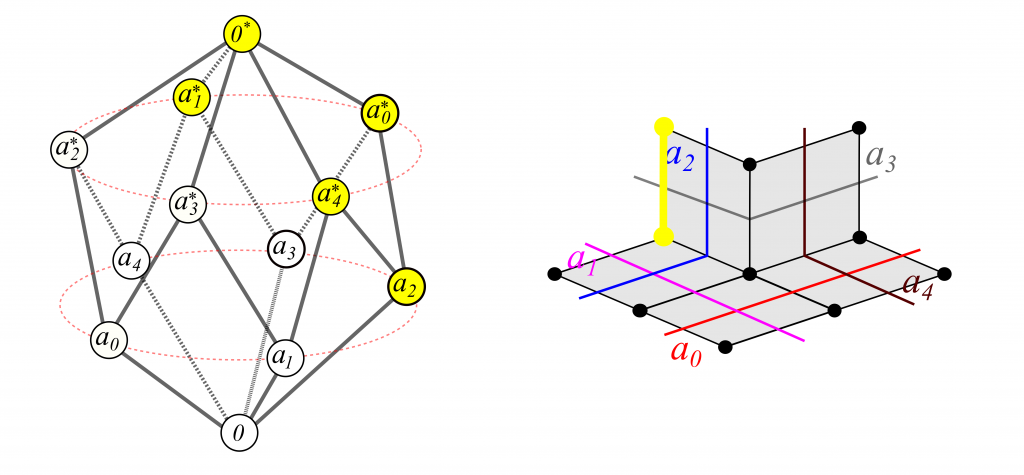
For a tangible example, consider two agents, A and B, each observing the same compass, whose needle (with state space the unit circle) points in the direction of one’s deepest desire 😉
Both agents consider only the queries:
n (/s/e/w): “Is the needle pointing North (/South/East/West)?”,
agreeing on the properties: n⇒¬s and e⇒¬w. The agents differ in their activation fields for these queries, however, as described by the figure below, on its left hand side:
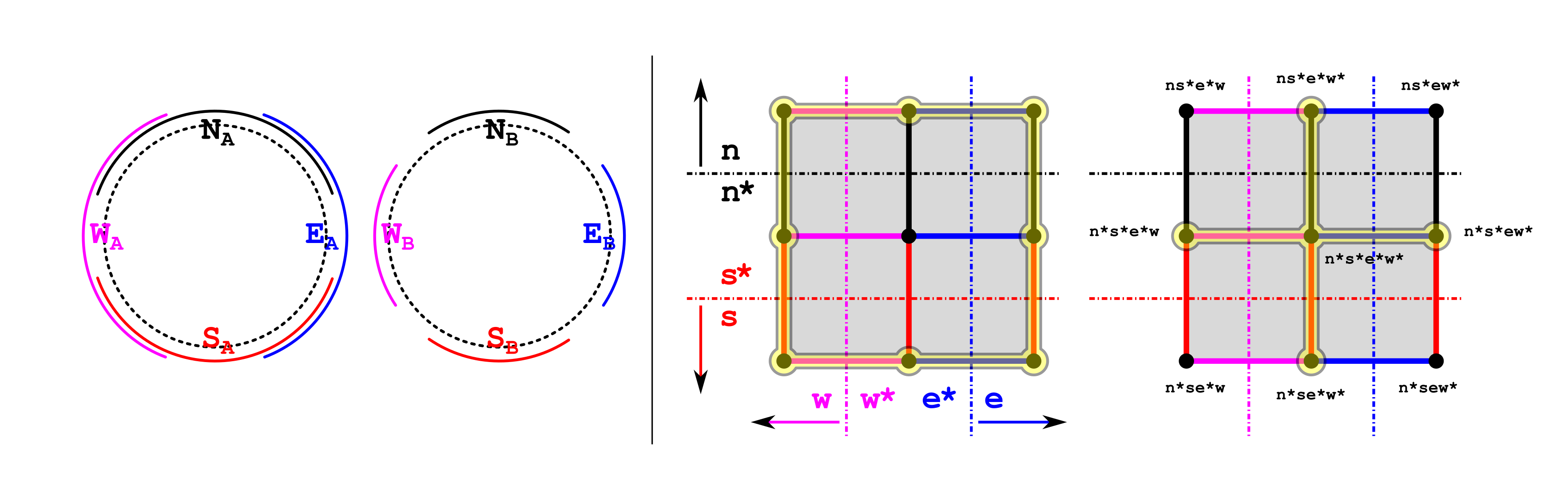
With their world of possibilities limited to the vertices of the four-dimensional cube of truth-value assignments to the set {n,s,e,w}, agents A and B will agree to deleting the vertices which violate their commonly accepted observations — as well as the faces of the 4-cube which touch these vertices — resulting in the cubical complex M on the right hand side of the figure.
The agents differ by which vertices — states of the world — they are able to experience, and the complex M represents their shared experience. Agent A seems to have a better chance of realizing that the actual state space of the compass needle has the homotopy type of a circle; Agent B will only ever witness it as a contractible space, being barred from distinguishing among the NE/NW/SE/SW directions. Furthermore, if learning is introduced, then given enough time to learn, Agent B might refine his set of rules to include n⇒¬e, n⇒¬w etc., improving the fit between its model space and its experience of reality.
Another example of a “record of implications” and its model space:
“Common Sense” Reasoning using Geometry of the Model Space
The big boon of using the model spaces M encoded by the “implication record” graphs Γ is that M comes equipped with a geometry facilitating scalable inference and planning in M. Specifically:
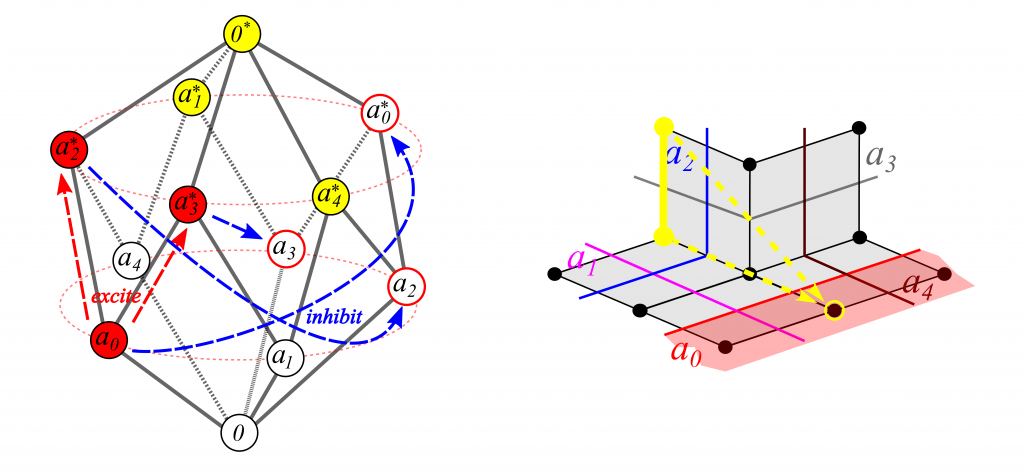
All convex subsets of M can be represented as implication-closed truth-value assignments to the vertices of Γ, which means that the model space M need not be realized in the agent’s memory — maintaining the graph Γ is enough — which brings representation costs (both in terms of space and in terms of time) down from exponential in the number of sensors to quadratic. Here is an example representation:
Nearest-point projection to any convex subset K of M is realizable via truth-value propagation along Γ (with inhibition of complements), which means that, at any time, the consequences of altering the truth values of specified queries from a specified current state may be computed in linear to sub-cubic time (in the number of sensors), depending on the implementation and on the hardware. Here is an illustration of projecting the state from the previous example to one of the “half-spaces”:
First Generation UMA agents
Funded in part by AFOSR CHASE MURI and in part by NSF-CABiR
Actions are Sensors in UMA agents.
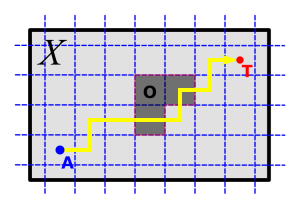
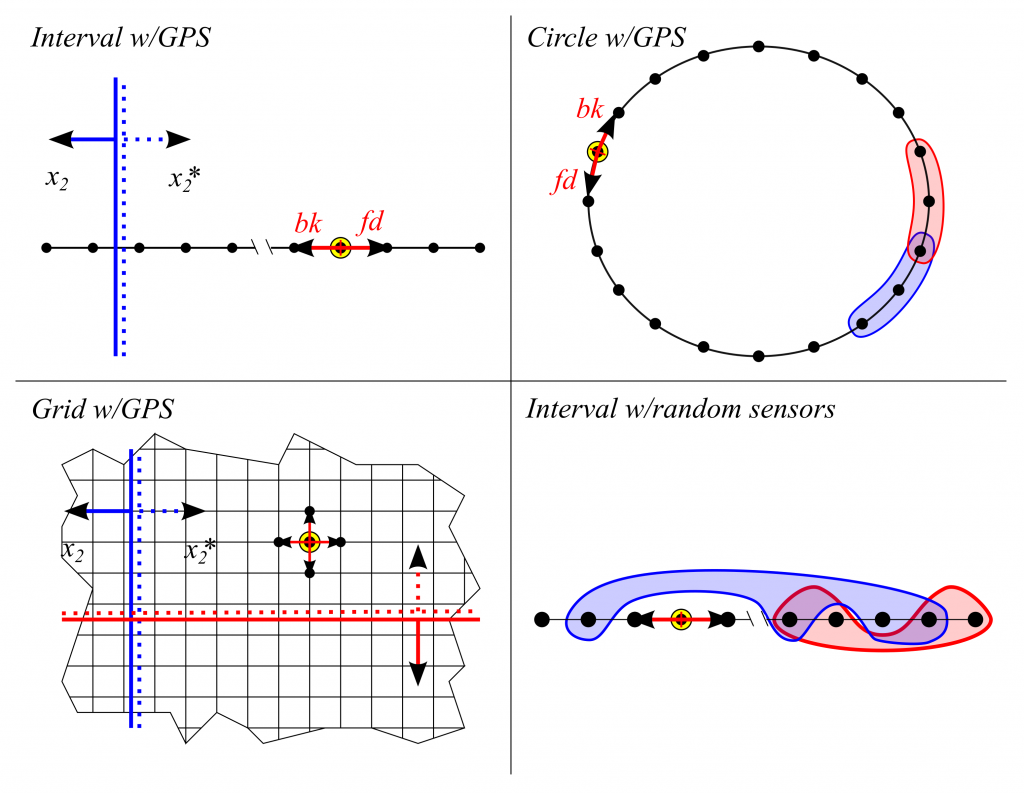
Achieving agency requires the introduction of actions and an ability to represent their consequences. Here is an example model space for an agent situated on a discrete interval with 6 positions, capable of taking one step at a time, in either the forward or backward direction:
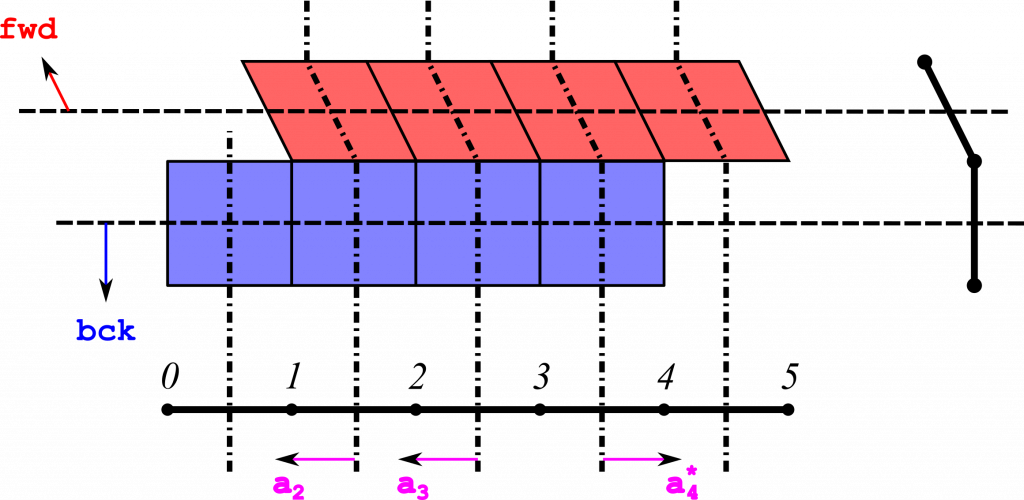
First Generation UMA Agents as Reactive Planners.
The 1st generation of UMA agents had actions introduced as controllable sensors, so that for each action α and every non-action sensor s the sensorium also contained the sensors α∧s and α*∧s, defined as the conjunction of α with the value of s in the preceding time step. Then implications of the form α∧s⇒t facilitate planning by producing a unified representation of both the environment and the immediate effect of actions in a single geometric object. Continuing the example of an agent moving along an interval:
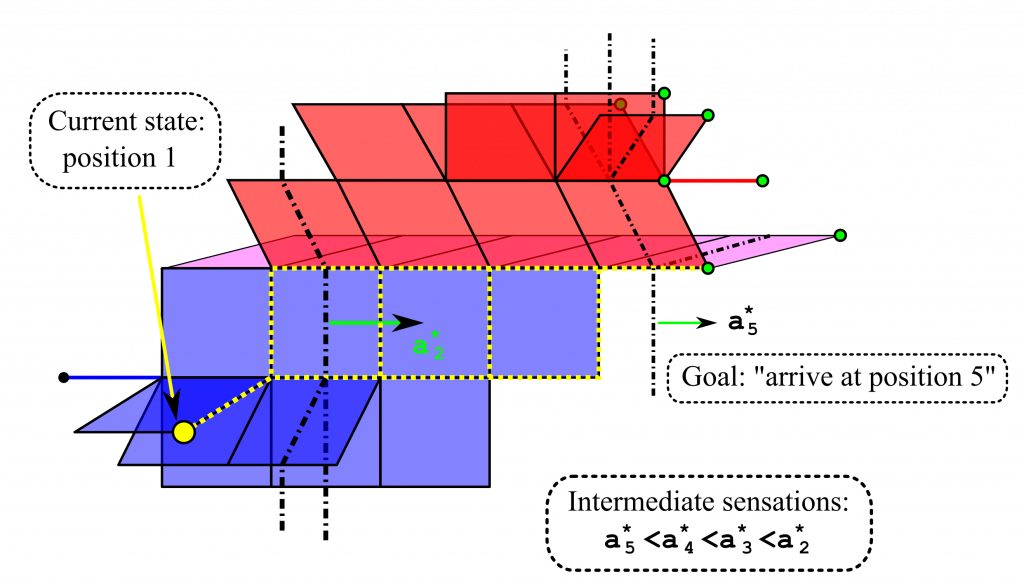
We show in [2] that, if a target state is given as a partial truth-value assignment T to Σ, then the unified representation effectively turns nearest point projection into a tool for gradient-surfing on information: for any truth-value assignment A to the action sensors, propagating the delayed conjunction of A with the current state C over the graph Γ produces a prediction of the next state; then one chooses A so as to minimize the distance (in M) of the predicted state to the desired state described by T. Computing this distance has linear time complexity.
“Sniffy” Agents: UMA-based Gradient Climbers.
We tested 1st generation UMA agents in a number of simulated settings, where an agent moves through a discrete environment attempting to learn the gradient of the distance function to the target: each agent was equipped with a sensor whose activation coincides with any decrease in the agent’s to the target; the target at any time was set to be the collection of states where this sensor is activated. In this sense, these agents are supposed to “sniff-out” the target — hence their name.
Varying (a) the topology/geometry of the environment, (b) implication-learning algorithms and their parameters, (c) the environment-sensing part of the sensorium, we considered the following settings:
Two types of learners were considered:
Empirical Learners, which accrue their weights as empirical probabilities of pairwise-synchronous activation;
Discounted Learners, which accrue weights as discounted filter estimates of the probabilities of pairwise-synchronous activation.
Both learners registered an implication a⇒b when the probability estimate for synchronous activation of a∧b* dropped below the uniform probability value of a single position in the environment.
Here are some results illustrating the efficacy of the learning and planning algorithms:
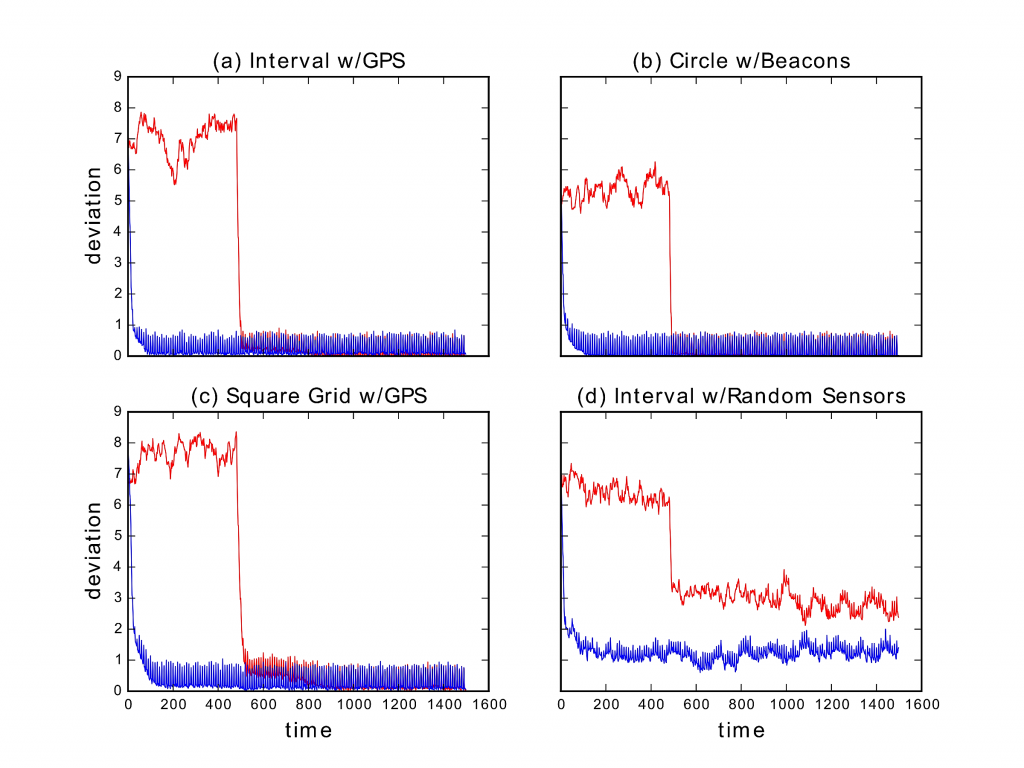
That a gradient climber could consistently reach a unique minimum is not at all novel. What is novel is that the gradient-climber is completely logic-based, moreover, the logic is learned together with the task. Implications representing each specific task may be unlearned as the agent tackles other tasks, while implications that are valid independently of the task (such as those encoding the environment’s geometry) will remain on record, forever affecting the geometry of the model space and thereby facilitating the learning of future tasks.
Fundamental Challenges.
1st-generation UMA agents are fundamentally limited in a variety of ways that are easily observed in Sniffy agents:
Inability to handle obstacles. The model spaces M are always contractible, and the planning mechanism makes extensive implicit use of this fact. As a result, “holes” in M, states which never materialize but must appear in M because of the way it is constructed — we call them essential obstacles — are bound to defeat the UMA greedy reactive planner.
Inability to handle independent sensors. Most interesting situations provide the agent with a collection of highly informative sensors, such as B/W cameras, where no two raw bits of output are correlated over the long term. In such a situations, a 1st-generation UMA agent will be unable to distill a collection of binary queries that’s of any use to the UMA planner. Hence the need in self-enrichment mechanisms extracting a meaningful collection of queries from the initial one.
Difficulty handling multiple synchronous actions. Finally, it seldom happens in Robotics (or, for that matter, in real life :-)) that an agent only has a few mutually-exclusive binary actions available. This turns the optimization step in the UMA planner into a serious problem in any real setting, calling for a more structured approach to organizing the agent’s “thinking” about actions.
Second Generation Agents; Communities.
With Daniel E. Koditschek, Siqi Huang (Penn CIS-CGGT masters program graduate) and Darius Rodgers (Penn ESE Junior)
Funded AFRL SIRCUS and DARPA “Lagrange”.
Motivating Idea: Topology in the Service of Bootstrapping.
1st-generation UMA agents are provably efficient and yield a minimalistic model space rich enough to account for all realizable states as well as for the homotopy type of the situation space. Yet, they are only effective when supplied with a sensorium Σ that is abundant in implications well-suited to the agent’s menagerie of basic actions. Moreover, essential obstacles further impede planning, like in the Sniffy-like setting depicted below:
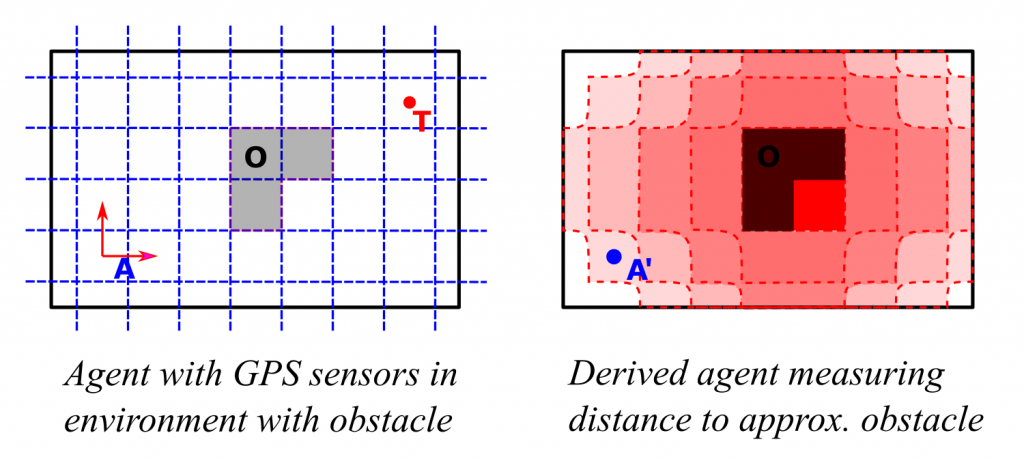
Our current research revolves around the idea of bootstrapping communities of UMA agents, starting from an initial set of UMA agents, each representing one of the available individual actions/behaviors of a single situated parent agent. The idea is to construct communities whose internal deliberations will guide the parent agent around the physical and logical obstacles in its problem space and towards learning and achieving its tasks — a society of minds much in the spirit of Marvin Minsky. In this context, if one thinks of each agent as maintaining some sort of “coordinate system” on situation space, a motor-action agent might respond to a planning failure by “spawning” a derived agent whose purpose is, for instance, to veto its parent agent whenever the robot gets too close to the state where this particular planning failure occurred:
The derived agent only needs to have some sensory endowment measuring this distance — sensors which are readily constructed from the internal deliberations of the parent agent.
In short, the approach is to leverage the unique mathematical features of the model spaces maintained by the individual agents for shaping the communal deliberation in a way that progressively improves the capacity of the system for generalization and identification of those essential obstacles in the situation space which obstruct UMA-based greedy navigation.
Means: Binary UMA Agents (BUAs)
To enable the rendering (and analysis) of complex action combinations/sequences, we switch to an architecture where each of an agent’s actions is seen as an independent agent, charged at any time with the binary decision whether to act or not to act:
- A BUA α maintains two UMA representations, the active snapshot (also indexed by α), representing information conditional on α being active, and the inactive snapshot (indexed by α*), whose contents are conditional on α being inactive.
- At time t, Each snapshot β∈{α,α*} computes:
- a current state representation Cβ from the raw binary observations, in the form of a non-empty convex set of its corresponding model space Mβ;
- a representation Tβ of the BUA’s target from the updated snapshot weights; the target set, too, is represented by a non-empty convex subset of Mβ;
- a representation Pβ of the BUA’s prediction of the next state, assuming β takes place.
- a divergence of the prediction from the target, is then computed (measured in bits, in terms of the geometry of the model space).
- Each BUA α decides whether to α or to α*, according to which divergence–the one computed by snapshot α or the one from α*, respectively–is smaller.
Learning from a Value Signal.
Separating the basic actions provides an opportunity for taking into account the possible distinctions between the environmental cues motivating different actions. If the BUA α is provided with a valuation φα(u) of its current sensory observation u, then thinking of the weight wab as an estimate of the expected value of the event a∧b one can:
- use UMA learning to omit [some] low value states from the world model, while increasing the chances of retaining information about rare high-value states, for example:
- generalized empirical weight update: wab is the sample mean of observed values of φα, approximating the expectation of φα over a∧b.
- generalized discounted weight update: analogously, wab is the discounted sample mean of observed values of φα.
- represent high value states by specifying a sensation a as more desirable than a* if its expected value (e.g. wa=wab+wab* in the examples above) is greater than that of a*;
- The resulting collection Tβ of target sensations turns out to always encode a non-empty convex subset of Mβ.
Qualitative Learning: a New Snapshot Type.
Since Pearl’s and Goldzmidt’s initial work on default systems (System-Z and System-Z+), the notion of a ranking function on the space of models for predicate logics has become central to the field of belief revision, mostly due to the seminal paper by Darwiche and Pearl.
Pearl established a formalism for deriving rules for default reasoning from “qualitative probabilities”, functions associating with each event (or, more generally, each formula) over an alphabet Σ a natural number describing the degree of its negligibility. (0 is not negligible, 1 is negligible, 2 is very negligible, 3–very very negligible, etc.)
In [3] we construct an UMA learning mechanism based on weights stated in this form and analyze its capabilities. So far, this has proven to be the most efficient and stable of the UMA learning mechanisms. The next figure illustrates this by comparing the evolution of the target representation over time, for different snapshot types:
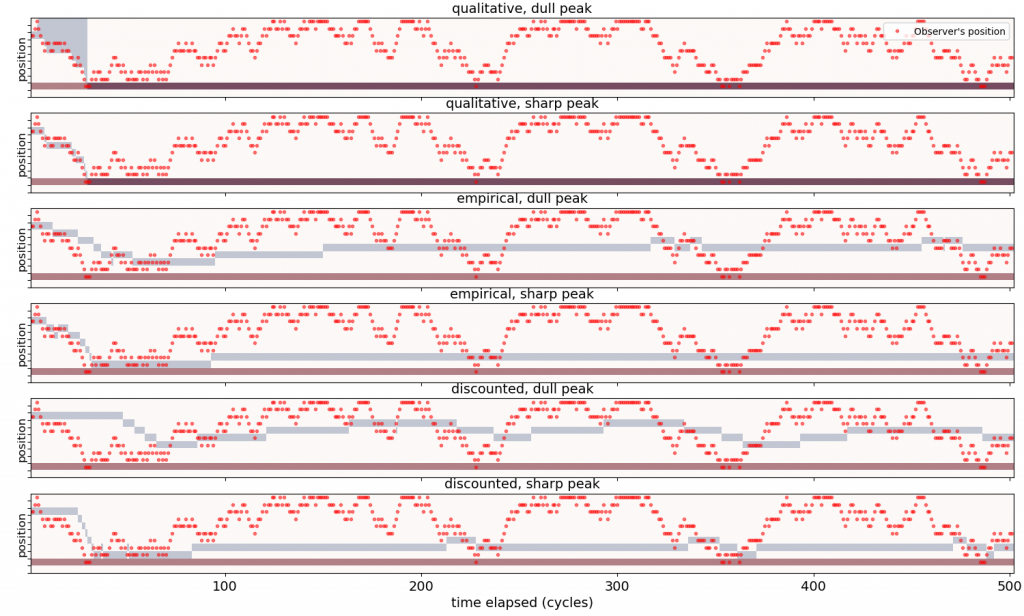
Implementing a “Society of UMA Minds” (UMA-SOM).
To facilitate experiments with a community of BUAs that could morph in real time, we are developing — thanks to immense help from Siqi Huang and AFRL SIRCUS funding– a simulation rig consisting of a Python-based front end managing a generic simulation environment (the scripts for which are also written in Python) which communicates, through REST, with a number of C++/CUDA back-end “listeners”, each realizing the computations done by a single BUA.
The current implementation makes it possible to realize autonomous sensory enrichment for each BUA separately, and makes it possible to add new BUAs during run time while endowing them with arbitrary sensors, including ones formulated in terms of internal computations of other BUAs, to facilitate the construction of critics. (Each BUA is “encapsulated” within a mini-environment of its own, which supplies its inputs and passes along its outputs).
Simulation Results with Simple UMA-SOM agents.
BUA version of Sniffy on the interval and circle.
In these simplistic discrete 1-dimensional environments with global positioning sensors, each agent is endowed with two BUAs, named fd (for making a step forward) and bk (for making a step back), with hard-wired arbitration: if the decision fd∧bk occurs, then one of these decision bits (determined by a coin flip) will be flipped before the decision is fed back into the environment. The BUAs fd,bk share a value signal that is a function of the distance (in steps) to a target. Same as before, the extremum of the value function may be more or less pronounced (“sharp/dull peak”).
Following a period of randomized exploration (a lazy walk), the BUAs are given control authority:
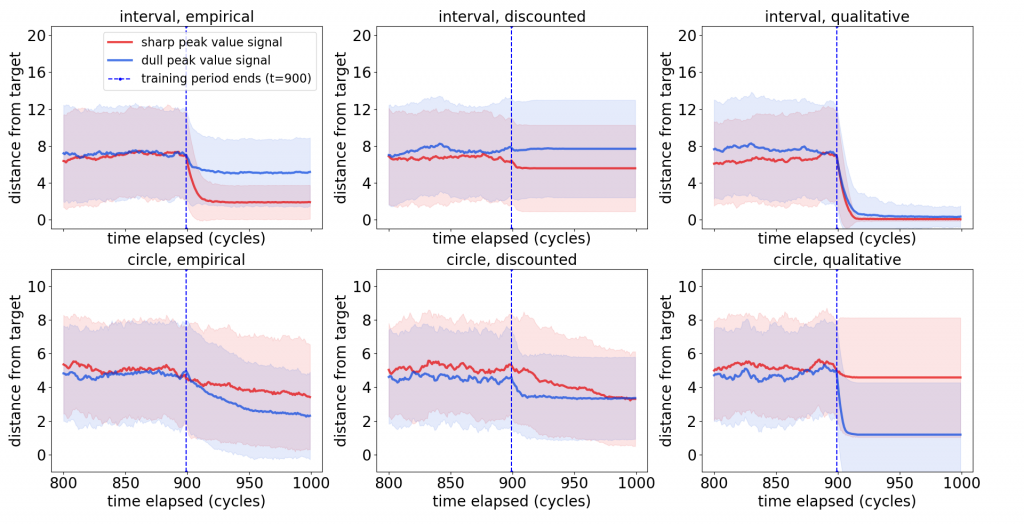
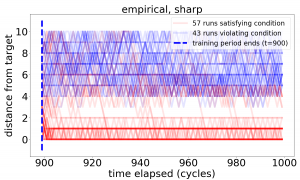
On the circle, plotting the distance to the target for all runs (instead of just the first two moments) provides more insight into the dynamics generated by the BUA decision engines:
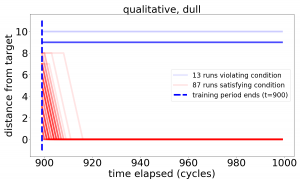
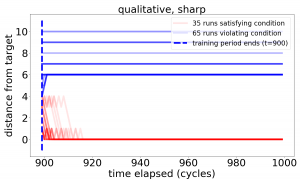
In the *dull* qualitative case, splitting the population of runs into those terminating closer to the target than to its antipode (red) and the rest (blue) yields a picture robustly consistent with gradient descent over the distance.
The *sharp* qualitative case does not behave as well. Our extended analysis in [3] explains the difference in terms of the learned implications: too many approximate implications become a burden on the decision-making system.
The other snapshot types exhibit similar tendencies, but are much less stable, due to the drift in the target representation and learned implications caused by the role of relative frequencies of observations in the accumulation of weights.
We are now working on characterizing a broad class of domains where “dull-peak” qualitative BUAs will be capable of learning navigation tasks.
Mice.
A slightly more complex, but more natural setting is that of an agent (referred to as “the mouse”) on the integer grid, capable of taking a step forward (fd), turning 90 degrees to the left (lt) or to the right (rt).
The environment (a subset of the integer grid) contains targets (“cheeses”), each contributing additively to a landscape, over which we would like the mouse to perform an approximation of gradient ascent.
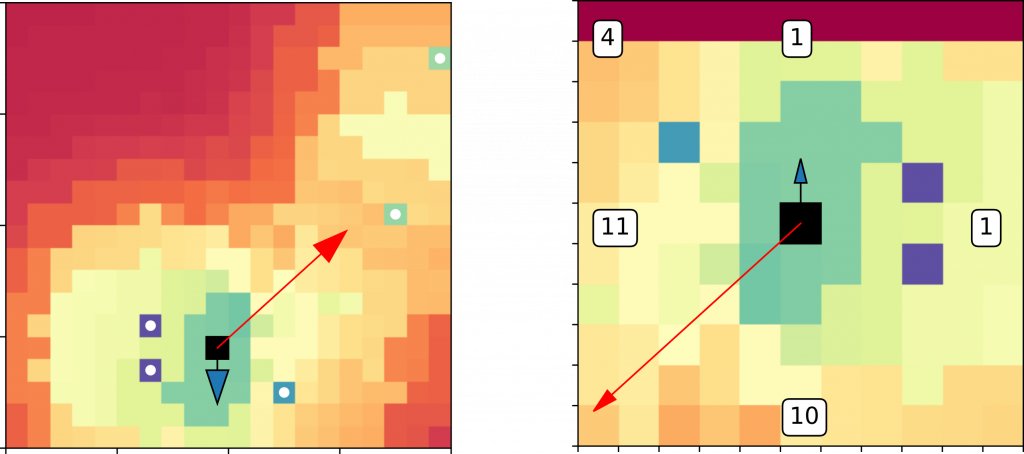
Intuitively, if the mouse is capable of querying a window (above, right) in the environment (above, left) regarding the angle of its pose vector to the gradient of the landscape (e.g. “is the gradient to my left?”, “is the gradient behind me?”), that should suffice for the BUAs lt,rt to learn to orient the mouse roughly along the gradient. Similarly, using differences in the landscape height to motivate the stepping BUA, fd, should suffice for it to conclude “if I am aligned with the gradient, I should make a step forward”.
The lt,rt pair of agents are clearly in a situation analogous to that of Sniffy on the circle, but with an extremely coarse discretization (4 positions in comparison to 20 in the preceding simulations), so we do expect some trouble. The question is just how much.
Moreover, in the discrete setting, turning and stepping do not commute, and must be arbitrated. We’ve applied the following arbitration: if the BUAs decide (lt∨rt)∧fwd, then a fair coin toss decides whether to step as decided, or to turn as decided. Of course, this can only contribute to variance in the simulation.
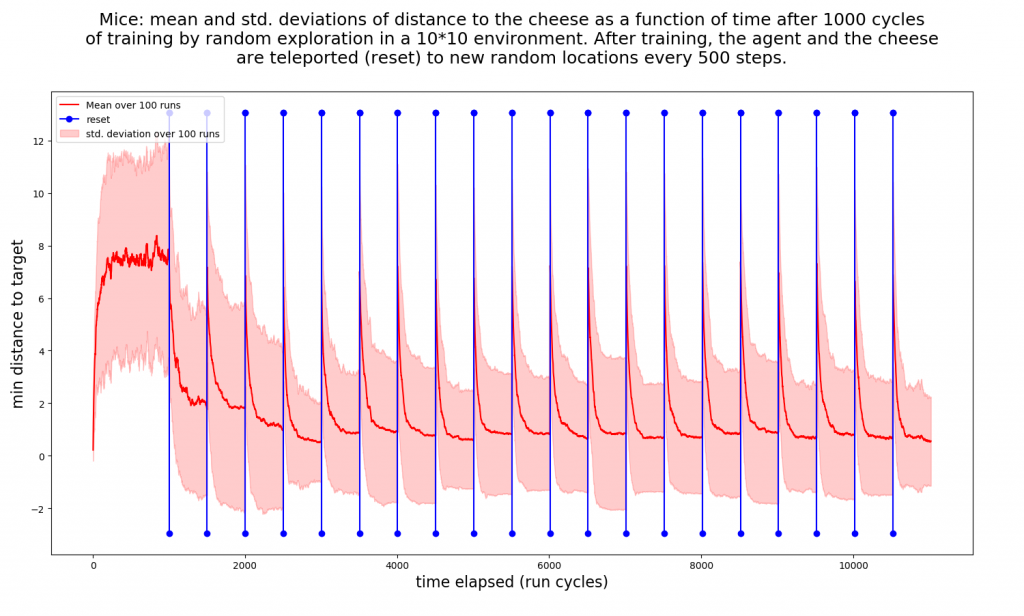
The simulation regimen we have run is as follows: after a training period of T cycles (random walk) in a rectangular 10×10 arena with a single stationary cheese, we set the mouse free for N training periods of R cycles each, where each training period begins with a reset: both the mouse and the cheese are teleported to random positions.
Here are the results for T=1000, R=500, N=20:
Next Steps
-
- Autonomous sensory enrichment. UMA representations autonomously modifying the set of queries Σ so as to improve the approximation of the true model space by the UMA model spaces.
- Learning to synchronize BUAs. Currently, BUAs are only capable of making selfish decisions which require hard-wired arbitration (such as in the Sniffy and Mice examples). We seek a uniform UMA-based method for bootstrapping autonomous task-dependent arbitration.
- Enable tracking of a moving target by qualitative BUAs. Qualitative snapshots are very efficient for target representation and implication-learning in a static setting, where the value signal–seen as a function of 2Σ –does not change over time. We seek to extend qualitative learning to the dynamical setting.