Functorial Hierarchical Clustering with Overlaps
with Jared Culbertson (AFRL) and Peter Stiller (Texas A&M)
More often than not, the word “classification” will relate to the task of assigning one of a set of prescribed labels to an incoming datum, resulting in a partitioning of the data acquired thus far into “blocks” consisting of data with identical output labels.
For example, consider the problem of producing a list of “object types” (chairs, tables, phones, toothbrushes…) present in an incoming VGA image, after training the classifier on a set of images of similar kind: with each image containing a certain number of objects of each type, the list of object types present, together with their counts may be seen as constituting a label. Two pictures with the same number of tables, chairs etc. will end up binned into the same block.
Alternatively, one might look for more structured classifiers, allowing two images to share a “block” if, say, both contain an object of the same type in sufficient quantity. In either case, one has to worry about consistency of the labels (the blocks) produced: what if the training set is changed? what if a filter is applied to the image, blurring some objects or their features and causing a misclassification?
In even more general learning settings where neither the number of possible labels nor their quality (the criteria for assigning them) are known, it then becomes preferable to submit to less restrictive notions of classification, which (1) forgo modeling the data as much as possible, replacing explicit comparison of prescribed features with implicit notions of dissimilarity between the data; (2) allow for different degrees of resolution, and (3) accept overlaps among emergent classes.
It is then natural to ask What mathematical guarantees are there of the consistency for the given classification algorithm, as one varies the training data? Moreover, What is the appropriate notion of consistency?
Our excursion into applying category-theoretic language to these problems has led us to surprising connections between dissimilarity-based clustering (flat or hierarchical) and isometric embeddings of data sets into minimal hyper-convex metric spaces (aka injective envelopes); to hyper-convex metrics on non-positively curved cubical complexes [2], and to new clustering methods affording overlaps and enjoying surprising consistency properties across data sets [1]. [Presentation]
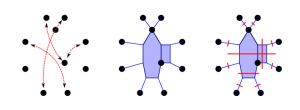
[1] “Functorial Hierarchical Clustering with Overlaps” (with Jared Culbertson and Peter F. Stiller) to appear in Discrete Applied Mathematics.
[2] “Injective metrizability and the duality theory of cubings” (with Jared Culbertson and Peter F. Stiller), to appear in Expositiones Mathematicae.
