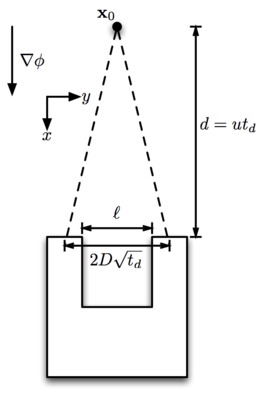
We develop a stochastic framework for modeling and analysis of robot navigation in the presence of obstacles. We show that, with appropriate assumptions, the probability of a robot avoiding a given obstacle can be reduced to a function of a single dimensionless parameter which captures all relevant quantities of the problem. This parameter is analogous to the Peclet number considered in the literature on mass transport in advection-diffusion fluid flows. Using the framework we also compute statistics of the time required to escape an obstacle in an informative case. The results of the computation show that adding noise to the navigation strategy can improve performance. Finally, we present experimental results that illustrate these performance improvements on a robotic platform.
For more information: Kod*Lab