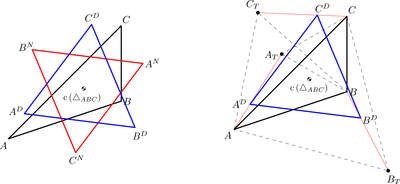
An elementary geometric construction, known as Napoleon’s theorem, produces an equilateral triangle, obtained from equilateral triangles erected on the sides of any initial triangle: The centers of the three equilateral triangles erected on the sides of the arbitrarily given original triangle, all outward or all inward, are the vertices of the new equilateral triangle. In this note, we observe that two Napoleon iterations yield triangles with useful optimality properties. Two inner transformations result in a (degenerate) triangle, whose vertices coincide at the original centroid. Two outer transformations yield an equilateral triangle, whose vertices are closest to the original in the sense of minimizing the sum of the three squared distances.
For more information: Kod*lab