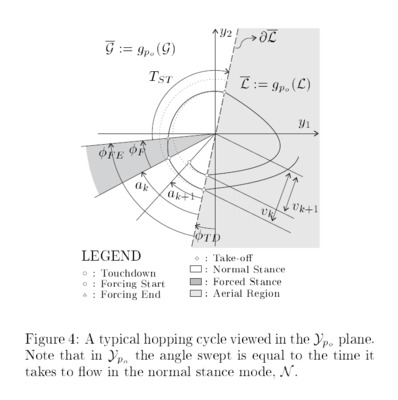
We investigate the stability of a one degree of freedom mechanical spring-mass system modulated by a feed-forward “clock” that stiffens and relaxes a Hooke’s law potential force according to a periodic rhythm. At the present early stage of inquiry, we offer sufficient conditions for local asymptotic stability of an isolated periodic orbit when there is no feedback to the clock at all but some viscous friction in the mechanism. We conjecture that, absent feedback, a lossless mechanical system cannot exhibit an asymptotically stable limit cycle in response to such rhythmic excitation.