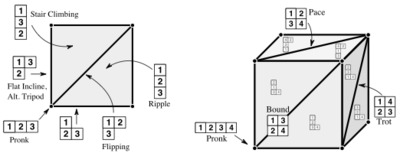
As robot bodies become more capable, the motivation grows to better coordinate them—whether multiple limbs attached to a body or multiple bodies assigned to a task. This paper introduces a new formalism for coordination of periodic tasks, with specific application to gait transitions for legged platforms. Specifically, we make modest use of classical group theory to replace combinatorial search and optimization with a computationally simpler and conceptually more straightforward appeal to elementary algebra. We decompose the space of all periodic legged gaits into a cellular complex indexed using “Young Tableaux”, making transparent the proximity to steady state orbits and the neighborhood structure. We encounter the simple task of transitioning between these gaits while locomoting over level ground. Toward that end, we arrange a family of dynamical reference generators over the “Gait Complex” and construct automated coordination controllers to force the legged system to converge to a specified cell’s gait, while assessing the relative static stability of gaits by approximating their stability margin via transit through a “Stance Complex”. To integrate these two different constructs—the Gait Complex describing possible gaits, the Stance Complex defining safe locomotion—we utilize our compositional lexicon to plan switching policies for a hybrid control approach. Results include automated gait transitions for a variety of useful gaits, shown via tests on a hexapedal robot.