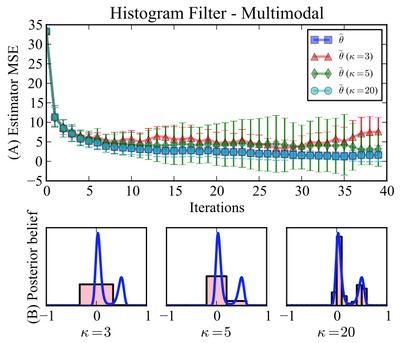
We prove convergence of an approximate Bayesian estimator for the (scalar) location estimation problem by recourse to a histogram approximant. We exploit its tractability to present a simple strategy for managing the tradeoff between accuracy and complexity through the cardinality of the underlying partition. Our theoretical results provide explicit (conservative) sufficient conditions under which convergence is guaranteed. Numerical simulations reveal certain extreme cases in which the conditions may be tight, and suggest that this procedure has performance and computational efficiency favorably comparable to particle filters, while affording the aforementioned analytical benefits. We posit that more sophisticated algorithms can make such piecewise-constant representations similarly feasible for very high-dimensional problems.
For more information: Kod*Lab